Le langage MATLAB

Il est possible d’enregistrer la session Matlab avec la commande diary. Ainsi la commande diary nom_du_fichier démarre l’enregistrement de la session dans le fichier intitulé nom_du_fichier du répertoire courant : tout ce qui est affiché dans la fenêtre de commande, après la commande diary nom_du_fichier, est inscrit dans le fichier nom_du_fichier. Si le fichier nom_du_fichier existait auparavant, l’écriture se fait à la suite de ce qui était déjà écrit. On peut aussi ensuite désactiver et réactiver l’enregistrement dans le fichier nom_du_fichier par les commandes diary off et diary on.

a=hilb(2)

a =

1.0000 0.5000

0.5000 0.3333

diary essai1.txt %enregistrement de la session sous le fichier: essai1.txt

%A partir de là, tout ce qui est écrit, est enregistré dans essai1.txt

a

a =

1.0000 0.5000

0.5000 0.3333

b=hilb(3)

b =

1.0000 0.5000 0.3333

0.5000 0.3333 0.2500

0.3333 0.2500 0.2000

diary off

c

c =

1.0000 0.5000 0.3333 0.2500

0.5000 0.3333 0.2500 0.2000

0.3333 0.2500 0.2000 0.1667

0.2500 0.2000 0.1667 0.1429

Le nom du répertoire courant s’obtient par la commande pwd et la liste des chemins d’accès où Matlab cherche les fonctions appelées s’obtient par la commande path. On change de répertoire courant à l’aide de la commande cd.

a=hilb(2)

a =

1.0000 0.5000

0.5000 0.3333

diary essai1.txt %enregistrement de la session sous le fichier: essai1.txt

%A partir de là, tout ce qui est écrit, est enregistré dans essai1.txt

a

a =

1.0000 0.5000

0.5000 0.3333

b=hilb(3)

b =

1.0000 0.5000 0.3333

0.5000 0.3333 0.2500

0.3333 0.2500 0.2000

diary off

c

c =

1.0000 0.5000 0.3333 0.2500

0.5000 0.3333 0.2500 0.2000

0.3333 0.2500 0.2000 0.1667

0.2500 0.2000 0.1667 0.1429

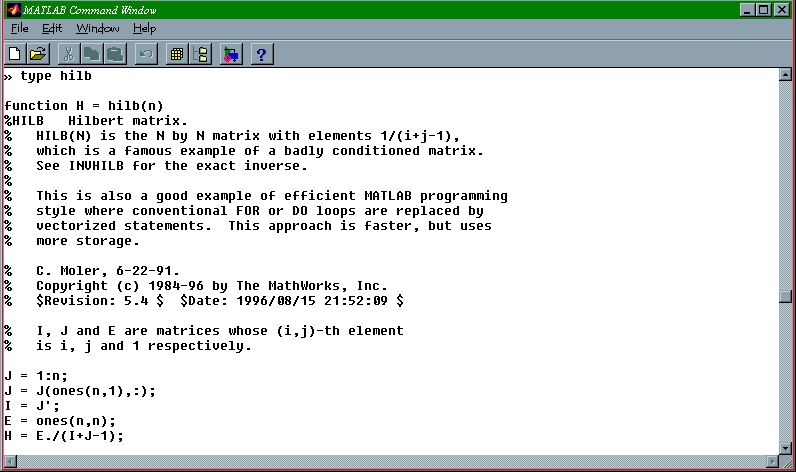
help hilb

HILB Hilbert matrix.

HILB(N) is the N by N matrix with elements 1/(i+j-1),

which is a famous example of a badly conditioned matrix.

See INVHILB for the exact inverse.

This is also a good example of efficient MATLAB programming

style where conventional FOR or DO loops are replaced by

vectorized statements. This approach is faster, but uses

more storage.

Matlab peut être utilisé en mode interactif, avec la ligne de commande. Dans les exemples ci-dessus, on a affecté – par exemple – à la variable a la matrice de Hilbert de taille 2.

Il est possible de supprimer l’affichage par l’ajout en fin de ligne de commande d’un : " ; "

En revanche, la commande disp est indépendante à la présence ou non de ce ; L’utilisation de la commande disp permet la suppression de l’affichage " a = "

On peut également demander de l’aide par les commandes help, type, … tapées directement sur la ligne de commande. La commande type hilb affiche dans la fenêtre de commande le contenu du fichier hilb.m. La commande help hilb donne le texte d’aide de la fonction hilb. Le texte d’aide commence à la première ligne débutant par le caractère % de hilb.m, et s’arrête à la première ligne qui ne commence pas par le caractère %.

L’espace de travail Matlab contient l’ensemble des variables qui peuvent être accessibles à partir de la ligne de commande. La commande who affiche le nom des variables de l’espace de travail, tandis que whos donne des précisions supplémentaires sur ces variables. Pour obtenir des informations sur une variable a, on pourra utiliser who a ou whos a.

La commande clear permet d’effacer les variables de l’espace de travail. La commande save permet de sauver le contenu de ces variables, ainsi que leur nom, dans un fichier binaire de nom matlab.mat situé dans le répertoire courant. La commande load permet de charger dans l’espace de travail les variables sauvées dans le fichier matlab.mat. On peut sauver plusieurs variables par une instruction du type save nomfich x y z, les variables x, y, z étant restaurés par la commande load nomfich dans le cas d’une sauvegarde par save nomfich x y z.

>> a=hilb(2);

>> b=hilb(3);

>> c=hilb(10);

>>

>> who

Your variables are:

a b c

>> whos

Name Size Bytes Class

a 2x2 32 double array

b 3x3 72 double array

c 10x10 800 double array

Grand total is 113 elements using 904 bytes

>> whos a

Name Size Bytes Class

a 2x2 32 double array

Grand total is 4 elements using 32 bytes

>> save

Saving to: matlab.mat

>> clear

>> a

??? Undefined function or variable 'a'.

>> load

Loading from: matlab.mat

>> a

a =

1.0000 0.5000

0.5000 0.3333

>>

>> save matrix a b c

>> clear

>> a

??? Undefined function or variable 'a'.

>> load matrix

>> a

a =

1.0000 0.5000

0.5000 0.3333

La commande format loose permet un affichage avec des lignes de blancs, alors que la commande format compact permet un affichage sans ces lignes de blancs. On peut d’ailleurs constater que la variable ans contient la dernière réponse non affectée. La commande format permet également de définir le mode d’affichage des chiffres. Le format short affiche les résultats en notation décimale, avec 4 décimales, de la forme ±c…c.dddd. Si un nombre est, en valeur absolue, plus grand que 1000 ou plus petit que 0.001, l’affichage exponentiel est adopté. Le format long est identique au précédent sauf qu’il compte 14 décimales. Pour les notations scientifiques, nous avons le format short e qui consiste en un affichage de la forme ±c.dddd e±^ppp avec 5 chiffres pour la mantisse et 3 chiffres pour l’exposant. La commande format long e permet un affichage analogue au précédent avec un codage sur 16 chiffres pour la mantisse. Notons enfin le format rat pour un affichage sous forme de fraction.

>> format loose

>> a=hilb(2)

a =

1.0000 0.5000

0.5000 0.3333

>> format compact

>> a=hilb(2)

a =

1.0000 0.5000

0.5000 0.3333

>> format short

>> pi

ans =

3.1416

>> format long

>> pi

ans =

3.14159265358979

>> format short e

>> pi

ans =

3.1416e+000

>> format long e

>> pi

ans =

3.141592653589793e+000

>> format rat

>> pi

ans =

355/113

Une matrice nulle peut être initialisée par la commande zeros

Une matrice unité peut être générée par la commande ones

Une matrice identité peut être construite par la commande eye

La fonction round représente l’entier le plus proche. La partie entière est représentée par la fonction floor.

La fonction linspace permet de générer un vecteur dont les termes sont équidistants.

On peut initialiser un vecteur ligne par les 2 commandes suivantes :

>> format compact

>> x=[1 2 3]; disp(x)

1 2 3

>> x=[1,2,3] %même chose sauf qu'on met des virgules

x =

1 2 3

>>

>> x=1:3

x =

1 2 3

>> %on ne précise pas le pas car par défaut c'est 1

>>

>> %Si le pas est différent de 1:

>> y=1:0.1:2

y =

Columns 1 through 7

1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000

Columns 8 through 11

1.7000 1.8000 1.9000 2.0000

Le vecteur colonne, transposé de x, s’initialise avec des points virgules ou par x’ :

>> z=[1;2;3]

z =

1

2

3

>> z=x'

z =

1

2

3

La dimension d’une matrice est donnée par la commande size, alors que la longueur d’un vecteur est donnée par la commande length :

>> a=[1 2 3;4 5 6]

a =

1 2 3

4 5 6

>> size(a)

ans =

2 3

>> %2 = nombre de lignes

>> %3 = nombre de colonnes

>>

>> v=[1;2;3;4;5;6]

v =

1

2

3

4

5

6

>> length(v)

ans =

6

La fonction sum appliquée à une matrice est le vecteur obtenu par sommation des colonnes de cette matrice. La fonction diag appliquée à une matrice carrée renvoie sa diagonale dans un vecteur.

>> a

a =

1 2 3

4 5 6

>> sum(a)

ans =

5 7 9

>> sum(a,2)

ans =

6

15

>> sum(a,1)

ans =

5 7 9

>> diag(a)

ans =

1

5

>> M=3*ones(4)

M =

3 3 3 3

3 3 3 3

3 3 3 3

3 3 3 3

>> diag(M)

ans =

3

3

3

3

On peut accéder aux éléments de la matrice a par une commande du type a(i,j) désignant le terme situé sur la i^ème ligne, j^ème colonne de a.

L’opérateur  ":" permet de créer des vecteurs mais aussi permet de donner le vecteur colonne des termes de a :

>> a

a =

1 2 3

4 5 6

>> a(2,1) %élément situé sur la 2ème ligne de la 1ère colonne

ans =

4

>> a(4) %4ème terme de a - les éléments sont alors numérotées colonne après colonne

ans =

5

>> a(1:4)

ans =

1 4 2 5

>> %On accède à plusieurs éléments de a

>> a(:)

ans =

1

4

2

5

3

6

Les fichiers M de commandes (appelés aussi fichiers scripts) sont des fichiers d’extension .m qui contiennent les mêmes expressions que celles de la ligne de commande. Ces fichiers n’ont pas d’arguments d’entrée ni de sortie et ils opèrent sur les variables de l’espace de travail.

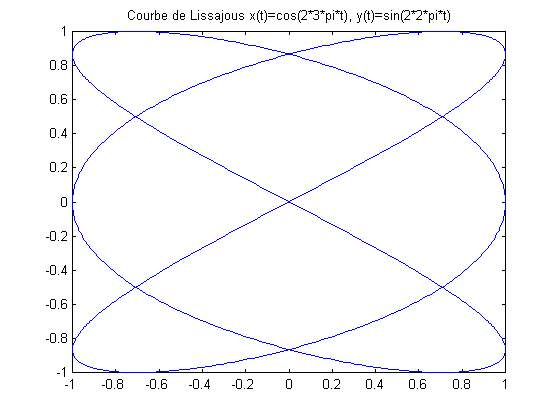
Exemple de fichier script avec les courbes de Lissajou.

On remarquera l’instruction " … " qui permet de couper une ligne.

La commande lissajou(3,2) tapée dans la feuille de commande de Matlab donne le graphique suivant :

Si p est un vecteur ligne ou colonne de taille n+1 de composantes (a_n , … , a_i , … , a₀), alors, dans Matlab, p représente aussi le polynôme de degré n : a_nxⁿ + … + a_ixⁱ + … + a₀x⁰

On remarque que p(1) est le coefficient de xⁿ, p(i) est le coefficient de x^n+1-i et p(n+1) le coefficient de x⁰ (puissances décroissantes).

L’instruction q=roots(p) renvoie le vecteur colonne des racines approchées de p. Une racine de multiplicité k figure alors k fois.

L’instruction p=poly(q) renvoie dans p un vecteur ligne représentant le polynôme dont les racines sont les termes de q.

L’instruction polyval(p,x) calcule et renvoie la valeur de p en x.

L’instruction q=polyder(p) renvoie un vecteur q qui est le polynôme dérivé de p et enlève les zéros qui pourraient apparaître au début de q ; q est un vecteur ligne.

Pour p et q vecteurs, l’instruction r=conv(p,q) renvoie le vecteur r du même type ligne ou colonne que p, des coefficients du polynôme produit p*q. Ensuite pour deux vecteurs p1, p2 de même type, [q r]=deconv(p1,p2) renvoie dans q et r le quotient et le reste de p1 par p2 : p1=p2.q + r

>> p=[1 2 1] %p=x²+2x+1

p =

1 2 1

>> q=roots(p)

q =

-1

-1

>> p=poly(q)

p =

1 2 1

>> polyval(p,0)

ans =

1

>> polyval(p,[0 1])

ans =

1 4

>> polyder(p)

ans =

2 2

>> p=[1 0 -1]; q=[1 0 1];

>> r=conv(p,q)

r =

1 0 0 0 -1

>> p1=[1 0 0 0 -1]; p2=[-1,0,-1];

>> [q,r]=deconv(p1,p2)

q =

-1 0 1

r =

0 0 0 0 0

Pour une matrice carrée a, l’instruction p=poly(a) renvoie dans p le vecteur ligne des coefficients du polynôme caractéristique de a. Pour un polynôme p, l’instruction polyvalm(p,a) renvoie la matrice p(a).

>> a=[2 -1;-1 2]

a =

2 -1

-1 2

>> p=poly(a) %polynôme caractéristique de a

p =

1.0000 -4.0000 3.0000

>> %Selon le théorème de Cauley-Hamilton p(a)=0 (0=matrice nulle)

Le dernier résultat est voisin de la matrice nulle, en effet la précision relative dans la représentation des réels par des nombres flottants pour ce logiciel est de l’ordre de : 2.2204 e ^–016.

Matlab représente la racine de –1 par i ou j. Pour un nombre complexe z, real(z) renvoie la partie réelle de z, imag(z) sa partie imaginaire, conj(z) son conjugué, angle(z) son argument tel que -p < angle(z) £ p et abs(z) son module. Ces fonctions s’appliquent à des tableaux : si a est une matrice à coefficients complexes et f une des fonctions précédentes, alors f(a) est la matrice de termes f(a_ij).

Une fonction mathématique peut être définie avec un fichier d’extension .m, mais aussi avec la commande inline qui permet de créer une variable de classe object inline.

Une représentation de fonctions de fonctions peut se faire par la commande fplot. Elle peut être utilisée sur des fonctions définies par un inline, sur des fonctions built-in (cos, sin, …) ou sur des fonctions définies par un fichier M.

>> f=inline('(x^2+x-1)/(x^2+2)')

f =

Inline function:

f(x) = (x^2+x-1)/(x^2+2)

>> whos f

Name Size Bytes Class

f 1x1 850 inline object

Grand total is 50 elements using 850 bytes

>> fplot(f,[-5,5])

>> title('(x²+x-1)/(x²+2)');

On obtient alors le graphique suivant :

>> x=-pi:0.01:pi;

>> y=sin(x);

>> plot(x,y);

On peut tracer plusieurs courbes à la fois. L’instruction plot de la séquence suivante:

>> y2=sin(x-0.5);

>> y3=sin(x+0.5);

>> plot(x,y,x,y2,x,y3);

efface la courbe de la fenêtre graphique n°1 et trace le nouveau graphe dans cette fenêtre. On remarquera le choix d’abcisses identiques.

On peut aussi spécifier la couleur, le style de la ligne et les marques de la courbe, comme nous le présente la figure suivante obtenue par :

La couleur rouge et les marques o sont obtenues par ¢ro¢, la couleur verte, le style " tirets " et la marque + sont obtenues par ¢g:+¢. On consultera le help pour les autres spécificateurs de couleurs, de styles de lignes et de marques.

La fonction plot crée, s’il n’en existe pas, une fenêtre graphique n°1, et, par défaut, utilise la fenêtre courante s’il en existe une. De nouvelles fenêtres graphiques, numérotées, peuvent être ouvertes avec la commande figure. La commande figure(n) permet alors de se positionner sur la fenêtre de numéro n, qui devient la fenêtre courante (si cette fenêtre n’existe pas elle est alors créée et a pour numéro n). Le résultat des commandes graphiques qui suivent est alors affiché dans cette fenêtre. La commande close permet de fermer la fenêtre courante.

La fonction hold permet d’ajouter un graphe à un graphe existant, par la commande hold on. La commande hold off permet de revenir à l’ancien mode.

>> x=-pi:0.01:pi;

>> y=cos(x);

>> plot(x,y)

>> hold on

>> y2=sin(x);

>> plot(x,y2);

La fonction axis possède de nombreuses options de gestion des axes. Nous en présentons 3. Sur la fenêtre graphique courante, l’instruction axis([xmin, xmax, ymin, ymax]) donne la fenêtre du graphe, l’instruction axis equal met les axes à la même échelle et la commande axis normal annule l’effet de la commande précédente.

La commande grid on permet de mettre une grille sur le graphe et la commande grid off enlève cette grille.

L’instruction zoom(x) permet un changement d’échelle d’un facteur x. La commande zoom on permet de zoomer avec la souris dans les différentes fenêtres graphiques. On désactive ce mode par la commande zoom off.