
Chapitre 9 : Cercles, triangles, quadrilatères


Un cercle est formé de tous les points situés à une même distance d’un point appelé centre. On appelle disque l’intérieur du cercle.
a/ Rayon – Diamètre – Corde :
|
[OC], [OA], [OB] sont des rayons du cercle [AB] est un diamètre du cercle [MN] est une corde |
|
b/ Tangente :
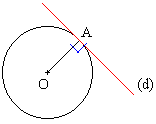
La droite (d) est la tangente en A au cercle. Elle a un seul point d’intersection avec le cercle : c’est le point A. De plus on a : (d) ^ (OA).
ATTENTION :
On peut décrire un cercle de différentes manières :
|
C est le cercle de centre O passant par AC est le cercle de centre O et de rayon [OA]C est le cercle de centre O et de rayon 2 cm |
|
Un
triangle est une figure à trois côtés et dont la somme des angles vaut 180°.|
Triangle rectangle |
Triangle isocèle |
Triangle équilatéral |
|
Un triangle rectangle a deux côtés perpendiculaires. Un triangle rectangle a un angle droit.
|
Un triangle isocèle a deux côtés de même longueur. On les repère sur le dessin par les petits traits rouges.
|
Un triangle équilatéral a trois côtés de même longueur. On les repère sur le dessin par les petits traits rouges.
|
Un
quadrilatère est une figure qui a quatre côtés.On parle de côtés opposés pour les 2 côtés qui se regardent, qui sont face à face.
On parle de côtés consécutifs pour 2 côtés qui ont un sommet en commun.
|
[AC] et [BD] sont les diagonales du quadrilatère ABCD ou du quadrilatère ADCD … A, B, C, D sont les sommets du quadrilatère. |
|
Quelques quadrilatères particuliers :
|
Trapèze |
Parallélogramme |
Losange |
Rectangle |
Carré |
|
Un trapèze a deux côtés parallèles.
|
Un parallélogramme a ses côtés opposés parallèles.
|
Un losange a quatre côtés de même mesure et des diagonales perpendiculaires.
|
Un rectangle a quatre angles droits.
|
Un carré a quatre angles droits, quatre côtés de même mesure et des diagonales perpendiculaires.
|
Un carré est à la fois un losange et un rectangle.
Un losange a ses diagonales qui se coupent en leur milieu tout comme le rectangle et le carré.
|