Chapitre 10 : Symétrie axiale

 

 

  1. FIGURES SYMETRIQUES :

    2. Deux figures sont symétriques par rapport à un axe, si en pliant suivant l’axe, les deux figures se superposent.

    Exemples :

    1er cas :

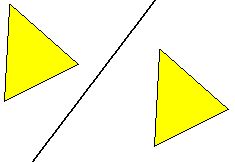
    Les 2 triangles ne sont absolument pas symétriques car si on plie le long de l’axe on aurait la figure suivante :

    2ème cas :

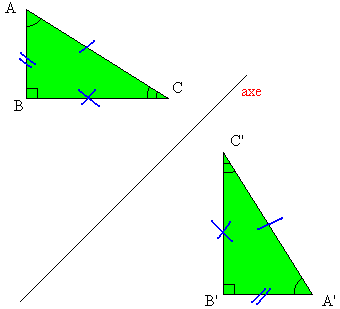
    Le point B¢ est le symétrique du point B.

    Le point A¢ est le symétrique du point A.

    Le point C¢ est le symétrique du point C.

    Les triangles A¢ B¢ C¢ et ABC sont symétriques et ont la même aire.

    Lorsque 2 figures sont symétriques : les mesures de longueur sont égales, les mesures d’angle sont égales et les mesures d’aire sont égales.

     

  2. AXES DE SYMETRIE :

    3. a/ Une figure peut avoir un ou plusieurs axes de symétrie :

    Un axe de symétrie

    Plusieurs axes de symétrie

    Exemple : un triangle isocèle

    Exemple : un rectangle

    A votre avis un losange a combien d’axes de symétrie ? Et un carré ? Et un cercle ?

    b/ Une figure peut ne pas avoir d’axe de symétrie :

    Par exemple, un triangle quelconque n’a pas d’axe de symétrie, un quadrilatère quelconque non plus.

     

  3. MEDIATRICE D’UN SEGMENT :

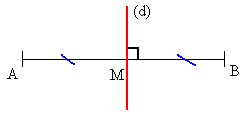
    4. La médiatrice (d) d’un segment [AB] est la droite perpendiculaire à [AB] qui passe par le milieu M de [AB].

    La médiatrice (d) du segment [AB] est un axe de symétrie du segment [AB].

     

  4. BISSECTRICE D’UN ANGLE :

    5. La bissectrice d’un angle est la droite qui partage cet angle en deux angles de même mesure.

    Exemple :

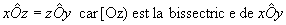    . La bissectrice de [Oz) est un axe de symétrie.

Suite du Cours