Chapitre 3 : Division et Problèmes

1. DIVISION EUCLIDIENNE :

   Effectuer une division euclidienne c’est trouver deux nombres entiers : le quotient et le reste.

   

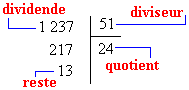
   On a alors : 1 237 = 51 ´ 24 + 13 et 13 < 51

   Dividende = diviseur ´ quotient + reste et le reste est toujours strictement inférieur au diviseur

   ATTENTION :

   • Dans une division euclidienne, le quotient est toujours un nombre entier.

   • On ne peut pas diviser un nombre par 0.

    

2. DIVISEUR, MULTIPLE :

   a/ Définition :

   Si le reste de la division euclidienne d’un entier a par un entier b est zéro on dit que :

   a est divisible par b

   b est un diviseur de a

   a est un multiple de b

   
   

   b/ Critères de divisibilité :

   Un nombre entier est divisible par 2 si son chiffre des unités est un multiple de 2 : 0, 2, 4, 6, 8

   Exemple : 12 578 est divisible par 2 car 8 est un multiple de 2 (8 = 4 ´ 2)

   Un nombre entier est divisible par 5 si son chiffre des unités est 0 ou 5

   Exemple : 78 500 est divisible par 5 car son chiffre des unités est 0

   Un nombre entier est divisible par 3 si la somme de ses chiffres est divisible par 3

   Exemple : 55 557 est divisible par 3 car 5 + 5 + 5 + 5 + 7 = 27 et 27 est divisible par 3 (27 = 3 ´ 9)

   Un nombre entier est divisible par 9 si la somme de ses chiffres est divisible par 9

   Exemple : 1 143 est divisible par 9 car 1 + 1 + 4 + 3 = 9 et 9 est divisible par 9

   On remarque qu’un nombre divisible par 9 est divisible par 3 ; en revanche un nombre divisible par 3 n’est pas forcément divisible par 9 :

   55 557 est divisible par 3 et 9 (55 557 = 9 ´ 6 173 = 3 ´ (3 ´ 6 173)) mais 381 n’est divisible que pas 3 (381 = 3 ´ 127).

    

3. QUOTIENT DE NOMBRES DECIMAUX :

   a/ Exemple :

   42 ´ 2,5 = 105.

   2,5 est le quotient de 105 par 42 et on écrit : 2,5 = 105 : 42

   
   

   b/ Définition :

   b ´ […] = a (b ¹ 0)

   Le nombre […] est le quotient de a par b. Il est noté a : b ou a/b (écriture fractionnaire du quotient).

   ATTENTION :

   Le quotient de 2 nombres décimaux n’est pas toujours un nombre décimal

   Exemple :

   10 : 3 n’est pas un nombre décimal 

   

   
   

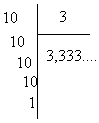
   c/ Propriété :

   On ne change pas le quotient de deux nombres si on les multiplie par un même nombre non nul, en particulier par 10, 100, 1 000, …

   Cette propriété permet de transformer la division de deux nombres "  à virgule " en une division de deux nombres entiers.

   Exemples :

   16,3 : 3,71 = 1 630 : 371

   14,7 : 5 = 147 : 50

   29,3 : 0,1 = 293 : 1 = 293

   
   

   d/ Division par 0,1 ; 0,01 ; 0,001 ;…

   Diviser un nombre par 0,1 ou 0,01 ou 0,001 revient à le multiplier par 10 ou 100 ou 1 000.

   Pour diviser un nombre décimal par 0,1 ou 0,01 ou 0,001, il faut décaler la virgule de ce nombre de 1 ou 2 ou 3 rangs vers la droite.

   Exemples :

   57,3 : 0,1 = 573

   8 745 : 0,01 = 874 500

   
   

4. VERIFIER LE RESULTAT D'UNE DIVISION EUCLIDIENNE:

   Pour vérifier si une division est exacte, il faut se poser 2 questions :

   • Est-ce que le reste est inférieur au quotient ?
   • Est-ce qu'on retrouve le dividende si on multiplie le quotient par le diviseur et qu'on ajoute le reste ?

   Exemple :

   Effectuer la division euclidienne de 1 234 par 45:

   

    

5. DETERMINER DES TRONCATURES OU DES ARRONDIS A L'UNITE:

   L'arrondi à l'unité d'un nombre est l'entier le plus proche de ce nombre

   Exemples :

   85,5 : 25 = 3,42

   TRONCATURE à l'unité du quotient de 85,5 par 25 : c'est 3.

   ARRONDI à l'unité du quotient de 85,5 par 25 : c'est 3.

   
   37 : 8 = 4,625

   TRONCATURE à l'unité du quotient de 37 par 8 : c'est 4.

   ARRONDI à l'unité du quotient de 37 par 8 : c'est 5.