Chapitre 6

Intégrales dépendant d’un paramètre

1. CAS DE L’INTEGRALE SUR UN SEGMENT I = [a,b] :

   Théorème de continuité sous le signe I  :

   Soit A une partie de ú ⁿ et f : A´ [a,b] ® ÷  : (x,t) ® f(x,t) une fonction continue sur A´ [a,b], alors :

   est une fonction continue sur A

   Théorème de dérivation sous le signe I  :

   Soit A un intervalle de ú et f : A´ [a,b] ® ÷  : (x,t) ® f(x,t) une fonction continue sur A´ [a,b]

   On suppose :

   1) " (x,t) Î A´ [a,b] (¶ f/¶ x)(x,t) existe

   Si x est sur le bord gauche de A :

   Si x est sur le bord droit de A :

   2) l’application est continue

   Alors : est de classe C¹ sur A et

   Remarque :

   Si A est un intervalle de ú contenant [c,d] et f une fonction continue de A´ [a,b] ® ÷   par application du théorème précédent à la primitive de F s’annulant en c il vient :

   

   Ce théorème de permutations des signes I n’est en fait qu’un cas particulier d’un théorème plus général sur les intégrales doubles : le théorème de Fubini.

 

2. CAS DE L’INTEGRALE SUR UN INTERVALLE QUELCONQUE : l’approche utilisant la Convergence Dominée :

I est maintenant un intervalle quelconque de ú , on note d_I = Inf(I) et f_I = Sup(I) ; on peut donc avoir d_I = - ¥ et f_I = +¥ .

On dit que l’application j  : I ® ÷ est une fonction continue par morceaux s’il existe un nombre fini de points a_i i=1..n : d_I £ a₁ < … < a_n £ f_I telle que :

1. j est continue sur chacun des sous intervalles ]d_I, a₁[, ]a_i, a_i+1[, ]a_n, f_I[
2. et

existent pour i=1..n

L’ensemble de telles fonctions sera noté C⁰_mrcx (I, ÷ ). On note aussi C⁰_mrcx (I, ú ⁺ ) les fonctions continues par morceaux sur I à valeurs positives.

Définition :

j Î C⁰_mrcx (I, ú ⁺ ) est dite intégrable sur I si l’ensemble { I _J j (x) dx ; J segment Ì I } est borné, on pose alors :



j Î C⁰_mrcx (I, ÷ ) est dite intégrable (au sens de Lebesgue) sur I si |j | l’est. Dans ces conditions, si (J_n)_n est une suite quelconque de segments inclus dans I, dont la réunion est I, on peut poser :



 

On montre que cette définition a un sens, de plus elle coïncide avec la précédente pour j Î C⁰_mrcx (I, ú ⁺ ).

Lemme de convergence sur un segment :

Soit (g_n)_n une suite d’applications continues par morceaux sur [a,b] à valeurs positives telles que :

1. (g_n)_n converge simplement vers 0
2. $ M > 0 tel que " x Î [a,b] : 0 £ g_n(x) £ M

alors :

 

Théorème de la convergence dominée :

Soit (f_n)_n une suite de C⁰_mrcx (I, ÷ ) telle que :

1. Il existe j intégrable sur I appartenant à C⁰_mrcx (I, ú ⁺ ) telle que " n Î ù , " x Î I : |f_n(x)| £ j (x)
2. Les (f_n)_n convergent simplement vers f Î C⁰_mrcx (I, ÷ )

Alors f et les (f_n)_n sont intégrables sur I et

 

Théorème de continuité sous le signe I  :

Soit A une partie de ú ⁿ et f une fonction continue de A´ I ® ÷  : (x,t) ® f(x,t).

S’il existe j Î C⁰_mrcx (I, ú ⁺ ), intégrable sur I, telle que :

" (x,t) Î A´ I |f(x,t)| £ j (t)

alors on peut définir l’application F : x ® F(x) = I _I f(x,t)dt de A dans ÷ et cette application est continue.

 

Théorème de dérivation sous le signe I  :

Soit A un intervalle de ú , non réduit à un point et f : A´ I ® ÷  : (x,t) ® f(x,t) une application continue. On suppose :

1. " (x,t) Î A´ I : (¶ f/¶ t)(x,t) existe (avec les conventions usuelles aux bords de A)
2. l’application : est continue
3. il existe 2 applications j ₀ et j ₁ Î C⁰_mrcx (I, ú ⁺ ), intégrables sur I telle que :

" (x,t) Î A´ I |f(x,t)| £ j ₀(t) ( domination pour f ) ( domination pour ¶ f/¶ t )

alors l’application F : x ® F(x) = I _I f(x,t)dt est définie et est de classe C¹ sur A et :

 

3. INTEGRALES DEPENDANT D’UN PARAMETRE : l’approche utilisant la convergence uniforme

Soient I un intervalle ouvert non vide réel et g : I´ [a ,b [ ® ÷ une fonction continue, a Î ú et b Î ú È {+¥ }. On peut bien sur avoir la même théorie en remplaçant [a ,b [ par ]a ,b ] où a Î ú È {- ¥ } et b Î ú .

Pour x Î I, on pose . A priori, f(x) n’existe pas ! !

Par contre si a est un nombre réel vérifiant a £ a < b , pour chaque x de I : existe en tant qu’intégrale de Riemann.

Le premier problème est de savoir si existe, auquel cas c’est cette valeur que l’on prend pour définir f(x).

Si f(x) existe pour tout x de I, le deuxième problème est de savoir si f : x ® f(x) est continue, intégrable, dérivable, etc… Ces propriétés résultent des propriétés des fonctions f_a : x ® f_a(x) définies sur I et du mode de convergence de f_a vers f.

1. Propriétés des fonctions f_a :

   Théorème de continuité :

   Sous les hypothèses précédentes, f_a est continue sur I

   Théorème de dérivation :

   Soit g continue, si (¶ g/¶ x)(x,t) est définie et continue sur I´ [a ,a] alors f_a est continûment dérivable sur I et, pour x Î I,

   Théorème d’intégration :

   Sous les hypothèses précédentes, f_a est Riemann intégrable sur tout intervalle [l ,m ] inclus dans I et :

   (Interversion des signes sommes)

    

2. Mode de convergence des fa vers f :

   a – Convergence simple en x Î I : (abrégé par C.S.)

   On dit que f_a converge simplement en un point fixé x de I, s’il existe une limite l telle que :

   " e > 0 $ h > 0 |a – b | < h Þ

   On remarque que en général h dépend de x

   On note bien sur f(x) = l =

   Comme ÷ est complet, pour que l’on ait convergence simple en x, il faut et il suffit que l’on ait le critère de Cauchy, c’est à dire :

   " e > 0 $ m > 0 |a – b | < m et |a¢ - b | < m Þ

   Là encore m dépend de x ! !

   b – Convergence absolue en x de I : (abrégé par C.A.)

   C’est la même notion, mais sur les fonctions :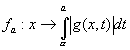

   Comme ÷ est complet, on obtient au moyen du critère de Cauchy : C.A. Þ C.S.

   c – Convergence uniforme sur I : (abrégé par C.U.)

   Si pour chaque x de I il existe un nombre f(x) tel que :

   " e > 0 $ h > 0 (indépendant de x !) " x Î I |a – b | < h Þ

   On dit que f_a converge uniformément vers f sur I lorsque a tend vers b .

   Pour qu’il en soit ainsi il faut et il suffit que l’on ait le critère de Cauchy uniforme :

   " e > 0 $ m > 0 (indépendant de x !) |a – b | < m et |a¢ - b | < m Þ

   d – Convergence normale sur I : (abrégé C.N.)

   On pose . On dit que f_a converge normalement sur I si l’intégrale est convergente. Autrement dit :

   " e > 0 $ m > 0 (indépendant de x !) |a – b | < m et |a¢ - b | < m Þ

   e – Comparaison des différents modes de convergence :

   

    

3. Propriétés de la fonction f :

Théorème de continuité :

Si f_a converge uniformément sur I vers f lorsque a tend vers b , alors f est continue.

 

Théorème de dérivabilité :

Si (¶ g/¶ x)(x,t) est définie et continue sur I´ [a ,b [, si les fonctions convergent uniformément sur I, et s’il existe x₀ Î I pour lequel tend vers f(x₀) lorsque a tend vers b , alors f est définie et est de classe C¹ sur I et : .

 

Théorème d’intégration :

Si les fonctions f_a convergent uniformément sur I lorsque a tend vers b , f est intégrable sur tout intervalle [l ,m ] Ì I et on a :

(Interversion du signe somme)