Chapitre 5
Fonctions différentiables de ún dans úp
f : Uouvert Ì ún ® úp
x Î U x = (x1, x2, …, xn) fixé
f(x) = f(x1, x2, …, xn) = (f1(x), f2(x), …, fp(x))
On définit :
C’est la ième dérivée partielle de f en x.
En posant : ei = (0,0,…,0,1,0,…,0) le ième vecteur de la base canonique, on peut écrire aussi :
On fixe toutes les composantes
sauf xi et on dérive par rapport à xi
Proposition :
(¶f/¶xi)(x) existe ó " j=1..p (¶fj/¶xi)(x) existent
(¶f/¶xi)(x) est le vecteur de composantes 
Remarque : Même si toutes les dérivées partielles existent en tout point de U, f n’est pas forcément continue.
Définition :
f : Uouvert Ì ún ® úp
f est de classe C1 sur U ssi " i=1..n (¶f/¶xi)(x) existe et est continue sur U
Proposition :
Si f est de classe C1, alors f est continue sur U.
Dérivation sous le signe somme dans le cas d’une intégrale de Riemann :
a < b I = [a,b] un intervalle compact de ú
f : [a,b]´U ® ú où U est un ouvert de ú
( t , x) ® f(t,x)
Proposition :
Si f est continue sur [a,b]´U et si ¶f/¶x existe et est continue sur I´U, alors :
g(x) = 
est dérivable sur
U et g¢(x) = 
Gradient, composition de fonctions dans un cas particulier :
f : Uouvert Ì ún ® ú
x = (x1, x2, …, xn) ® f(x)
Supposons " i=1..n (¶f/¶xi)(x) existe en x Î U
Définition :
Grad f(x) = Ñ f(x) = 
Proposition :
Si g : I ® ún est un arc paramétré C1 a valeurs dans U définie sur un intervalle ouvert I
t ® g(t)
F(t) = f(g(t)) est aussi de classe C1 et : F¢(t) = áÑ f(g(t)) , g¢(t)ñ (produit scalaire)
Introduction de la différentielle dans le cas le plus simple :
Soit g une application d’un ouvert U de ú2 à valeurs dans ú et (x0,y0) un point de U, on dit que g est différentiable en (x0,y0) s’il existe un nombre a > 0 et une application linéaire L de ú2 dans ú telle que pour tout (u,v) satisfaisant Ö(u²+v²) < a, on ait :
avec 
En faisant successivement (u,v) = (u,0) et (u,v) = (0,v) on voit nécessairement :
On adopte les notations usuelles :
L = différentielle de g en (x0,y0) est notée dg(x0,y0). La différentielle est une application linéaire et si elle existe, elle est unique.
L’application (u,v) ® u : 1ère projection : dx
L’application (u,v) ® v : 2ème projection : dy
De sorte que la formule précédente s’écrit
dans ú2* : 
Si g est maintenant, toujours définie sur U (ouvert de ú2) et à valeurs maintenant dans ú2 : g = (g1,g2)
On dira que g est différentiable en (x0,y0) si chacune de ses composantes l’est et on notera :
dg(x0,y0) = (dg1(x0,y0),dg2(x0,y0))
de sorte que la différentielle de g en (x0,y0) est entièrement caractérisée par la matrice suivante dite matrice jacobienne de g en (x0,y0) :
Le déterminant de cette matrice s’appelle le jacobien de g en (x0,y0) : Jg(x0,y0)
Différentiabilité :
Soit f une application d’un ouvert U de ún à valeurs dans úp, et x0 un point de U. On dit que f est différentiable en x0, s’il existe une application linéaire L de ún dans úp et un nombre strictement positif a tels que :
" h Î ún avec 2h2 < a on ait : f(x0+h) – f(x0) = L(h) + 2h2e(h) avec limh®0 e(h) = 0
L’application linéaire L : ún ® úp, si elle existe est unique, et nous la noterons df(x0). Elle est appelée la différentielle de f en x0.
Proposition :
Si f est différentiable en x0, alors f est continue en x0
Proposition :
L est définie de façon unique
L a pour matrice dans les bases canoniques la matrice jacobienne
Proposition :
f est différentiable en x0 ssi " j=i fj est différentiable en x0 :
Dérivée suivant un vecteur :
f : A Ì ún ® úp où A est une partie quelconque de ún
Soient x0, v Î A fixés
Définition :
On dit que v est un vecteur admissible en x0 (pour f relativement à A) s’il existe a > 0 tel que " t : 0 £ t £ a , x0 + t.v Î A (ou S[x0,x0+av] Ì A : le segment joignant x0 à x0+av est inclus dans A).
Soit donc v un vecteur admissible en x0
pour f, on appelle dérivée de f en x0
suivant le vecteur v, le vecteur de úp défini,
lorsque la limite existe, par :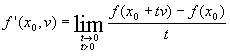 
En cas d’existence : " l ³ 0 : f¢(x0,lv) = l f¢(x0,v)
Proposition :
Si f est à valeurs réelles (i.e. p = 1) et si f¢(x0,v) existe, on a l’énoncé suivant :
Si f(x0) = Minloc x Î A f(x), alors f¢(x0,v) ³ 0 " vecteur v admissible
Lien avec la différentiabilité et les dérivées partielles :
Proposition :
Soit f : Uouvert Ì ún ® úp et x0 Î U
Si f est différentiable en x0, " v Î ún f¢(x0,v) existe et f¢(x0,v) = df(x0) v
La réciproque est fausse
Proposition :
Soit f : A Ì ún ® úp et x0 Î A
Si ei = (0,…,1,0,…0) le ième vecteur de base est admissible, de même que -ei, alors (¶f/¶xi)(x0) existe ó f¢(x0,ei) et f¢(x0,-ei) existent et f¢(x0,ei) = - f¢(x0,-ei)
Théorème :
Si f est de classe C1 (f a des dérivées partielles et elles sont continues) sur U alors f est différentiable en tout point de U.
La réciproque est vrai ! !
Condition nécessaire pour avoir un extremum local sur un ouvert :
Si f est différentiable en x0 et si f(x0) = Minloc xÎU , alors df(x0) = 0
THEOREMES PRINCIPAUX :
Théorème de composition :
Théorème :
Soit f : Uouvert Ì ún ® úp et x0 Î U f(U) Ì V
Soit g : Vouvert Ì úp ® úq et y0 = f(x0)
Si f est différentiable en x0, si g est différentiable en y0, alors : g·f est différentiable en x0 :
d(g·f)x0 = dgy0 . dfx0
De plus si f est de classe C1 sur U, si g est de classe C1 sur V, g·f est de classe C1 sur U
Théorème des accroissements finis :
1er cas : f est à valeurs dans ú :
Théorème :
f : Uouvert Ì ún ® ú différentiable
Soit a Î U, b Î U tel que S[a,b] Ì U
Si f est continu sur ce segment, il existe q Î ]0,1[ tel que :
f(b) – f(a) = df(a+q(b-a)) (b-a) = áÑf(a+q(b-a)) , b-añ
2ème Cas : pour p > 1 : f est à valeurs dans úp :
Théorème :
f : Uouvert Ì ún ® úp différentiable
Soit a Î U, b Î U tel que S[a,b] Ì U
On a seulement l’inégalité :
Corollaire :
Si f : Uouvert connexe Ì ún ® úp est différentiable et si " x Î U df(x) = 0 alors f = Constante
Théorème d’inversion locale :
Théorème :
f : Uouvert Ì ún ® ún on suppose f de classe C1 et soit x0 Î U
Si Jf(x0) ¹ 0 alors $ e > 0 tq f½B(x0,e[ soit un C1 difféomorphisme de B(x0,e[ sur son image f(B(x0,e[) qui est un ouvert de ún
Théorème des fonctions implicites :
Théorème :
Soit f une application de classe C1 de U´V (U : ouvert de ún , V : ouvert de ún) à valeurs dans ún
(x0,y0) est un point de U´V pour lequel l’application linéaire d2f(x0,y0), la différentielle en y0 de l’application partielle : y ® f(x0,y), est une bijection , alors il existe a > 0 et b > 0 tels que " x Î B(x0,a[ l’équation f(x,y) = f(x0,y0) admet une unique solution appartenant à B(y0,b[. De plus si on note y = g(x) cette solution, l’application g de B(x0,a[ dans ún est de classe C1.
Ce théorème affirme l’existence locale et théorique de la fonction g par contre g(x0) et dg(x0) sont parfaitement connus :
g(x0) = y0 et dg(x0) = - (d2f(x0,y0))-1 . (d1f(x0,y0))
d1f(x0,y0) est la différentielle en x0 de l’application partielle x ® f(x,y0)
d2f(x0,y0) est la différentielle en y0 de l’application partielle y ® f(x0,y)
Théorème de l’espace tangent :
Théorème :
Soit f : Uouvert Ì ún ® úp avec p ³ 1 une application de classe C1
Notons V = { x Î U ; f(x) = 0 } et prenons x0 Î V
On dit que v Î ún est tangent en x0 à V s’il existe une application C1 g : ]-a,+a[ ® ún telle que g(0) = x0 , " t Î ]-a,+a[ f(g(t)) = 0 et g¢(t) = v.
On note Tx0(V) l’ensemble des vecteurs tangents en x0 à V
Proposition :
Si df(x0) est surjective : Tx0(V) = Ker df(x0) et x0 est un point régulier de V
Corollaire :
Si p = 1 la condition df(x0) surjective se simplifie en Ñf(x0) ¹ 0
La conclusion peut s’exprimer en disant : v est alors tangent en x0 à V ssi v est orthogonal à Ñf(x0)
Fonctions de classe C2 :
f : Uouvert Ì ún
® ú est dite de classe C2 si " i " j Î {1..n},
les dérivées partielles secondes 
existent
et sont continues sur U. On appelle dans ce cas matrice
hessienne de f en x la matrice n´n :
Proposition :
La matrice hessienne est une matrice symétrique
Théorème : FORMULE DE TAYLOR LAGRANGE A L’ORDRE 2
Si f est une application de classe C2 sur un ouvert U de ún et si a et b sont 2 points de U tels que le segment S[a,b] soit contenu dans U il existe q Î ]0,1[ tel que :
f(b) – f(a) = áÑf(a) , b – añ + ½ t(b – a) Hf(a + q(b – a))(b – a)
Développement limité à l’ordre 2 : FORMULE DE TAYLOR – YOUNG :
Si f est une application de classe C2 sur un ouvert U de ún et si x0 appartient à U et h est un vecteur suffisamment petit :
f(x0 + h) = f(x0) + áÑf(x0) , hñ + ½ th Hf(x0)h + 2h2²e(h) avec lim h®0 e(h) = 0
Extrema sans contrainte :
Définition :
Soit f : Uouvert Ì ún ® ú différentiable, si x0 Î U satisfait Ñf(x0) = 0, on dit que x0 est un point critique de f.
Condition nécessaire d’extremum :
f : Uouvert Ì ún ® ú différentiable : si f(x0) = Minloc xÎU f(x), x0 est un point critique de f ; de plus si est de classe C2 les valeurs propres de la matrice hessienne Hf(x0) sont positives ou nulles.
Fonctions convexes différentiables :
Définition :
f : Cconvexe Ì ún ® ú est dite fonction convexe si :
" l Î [0,1], " x Î C, " y Î C f(lx + (1 – l)y) £ lf(x) + (1 – l)f(y)
Théorème :
f : Uouvert convexe Ì ún ® ú différentiable, f est convexe sur U ssi : " x Î U, " y Î U
áÑf(x) , y – xñ £ f(y) – f(x)
Corollaire :
Si f est convexe différentiable sur U ouvert convexe
f(x0) = Min xÎU f(x) ssi x0 est un point critique de f
Corollaire :
Si f : Uouvert Ì ún ® ú est différentiable, les conditions :
impliquent que f(x0) = Minloc xÎU f(x)
Proposition :
f : Uouvert Ì ún ® ú de classe C2, x0 Î U et B(x0,a[ Ì U
f½B(x0,a[ est convexe ssi les valeurs propres des matrices hessiennes Hf(x) pour x Î B(x0,a[ sont positives ou nulles
Proposition :
f : Uouvert Ì ún ® ú de classe C2, les conditions :
impliquent f(x0) = Minloc xÎU f(x) (ce Minloc est même strict)
Extrema avec contraintes d’égalité :
f : Uouvert Ì ún ® ú différentiable
g : U Ì ún ® úp de classe C1 g = (g1, g2, …, gp)
Définition :
On dit que x0 est un point régulier des contraintes K = { x Î U ; g(x) = 0 } si le système { Ñg1(x0), Ñg2(x0),…, Ñgp(x0) } est libre dans ún
Pour résoudre le problème Min xÎK f(x) on forme le Lagrangien du problème : L(x,l) = f(x) – ál,g(x)ñ qui est une fonction de U´úp dans ú.
Théorème :
Si f(x0) = Minloc xÎK f(x) ou f(x0) = Maxloc xÎK f(x) et si x0 est un point régulier des contraintes : il existe un vecteur l0 Î úp tel que ÑxL(x0,l0) = 0 ; de plus comme les contraintes sont satisfaites en x0 on a aussi : ÑlL(x0,l0) = 0 , donc si l’on préfère il existe l0 tel que : ÑL(x0,l0) = 0
Définition :
Les p composantes de l0 s’appelle les multiplicateurs de Lagrange en x0 du problème.
|
|
