Chapitre 4
Espaces vectoriels normés de dimension finie
Les espaces vectoriels de dimension finie, ce sont ceux qui ont une base ayant un nombre fini d’éléments.
Rappel sur la notion de norme sur un espace vectoriel :
Soit E un espace vectoriel sur ú . On appelle norme sur E une application N de E dans ú qui vérifie les 3 assertions suivantes :
PROPRIETES ELEMENTAIRES D’UNE NORME :
N(0) = 0 N(x) ³ 0 pour tout x de E
N(– x) = N(x) ½ N(x) – N(y)½ £ N(x + y)
L’égalité du parallélogramme n’a pas toujours lieu – elle caractérise les normes dérivant d’un produit scalaire.
Normes usuelles sur ú n :
Sur ú n on utilise couramment 3 normes : si x = (x1, … ,xn) désigne un vecteur de ú n , on pose :
N¥
(x) = 2
x2
¥
= 
N1 (x) = 2
x2
1 = 
N2 (x) = 2
x2
2 = 
On peut écrire aussi l’inégalité de Cauchy-Schwarz sous la forme suivante :
Boules définies à partir de N :
Boule ouverte unité : BN (x,1[ = { y Î E ; N(y – x) < 1 }
Boule fermée unité : BN (x,1] = { y Î E ; N(y – x) £ 1 }
Sphère unité : SN (x,1] = { y Î E ; N(y – x) = 1 }
Ces boules sont des convexes.
Définition :
N1 et N2 , 2 normes de E (e.v.)
" x Î E N1 ~ N2 ó $ a et b > 0 tq a N1 (x) £ N2 (x) £ b N1 (x)
Proposition :
N1 ~ N2 est une relation d’équivalence entre les normes sur un même espace.
Théorème :
Si E est un e.v. de dimension finie, toutes les normes sont équivalentes.
Remarque : Les notions topologiques ne dépendent pas de la norme choisie.
La propriété d’équivalence de 2 normes peut s’écrire également : 
pour tout x non nul de E. Donc si l’on appelle A l’ensemble des nombres réels de la forme N2(x)/N1(x), dire que les normes sont équivalentes signifie que A possède un majorant b et un minorant non nul a. Chercher les meilleurs constantes possibles, i.e. la plus grande constante a et la plus petite constante b revient à chercher la borne supérieure et la borne inférieure de l’ensemble A.
Applications linéaires – Normes d’endomorphisme :
Si B = { u1, …, un } est une base, l’application j
B : E ®
ú
n définie pour 
par j
B(x) = (x1, x2, …, xn) est non seulement un isomorphisme, mais aussi un homéomorphisme (j
B continue et bijective ; j
B–1 continue) : tous les espaces vectoriels normés de dimension finies se ressemblent : en particulier ils sont tous complets et vérifient le théorème de Bolzano – Weierstrass.
Soient E et F deux ú espace vectoriel de dimension finie. On note :
L(E,F) = {L : E ®
F linéaire} l’espace vectoriel (de dimension dimE ´
dimF) des applications linéaires de E dans F. On pose : 
où 2
.2
E [resp. 2
.2
F] est une norme de E [de F].
On dit ç ç ç . ç ç ç est la norme de L(E,F) associé à la norme ç ç . ç ç E et à la norme ç ç . ç ç F
Remarquons que : 2 L(x)2 F £ ç ç ç Lç ç ç . 2 x2 E
Si F = E on note End(E) = L(E,E) on a de plus pour L1 et L2 Î
End(E) :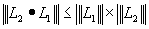 
On dit que la norme d’endomorphisme est une norme d’algèbre.
Proposition :
Si E = ú n et si on identifie End(E) aux matrices carrées à coefficients réels Mn´ n(ú ) :
Pour A Î Mn´ n(ú ) : A = (aij) i=1..n (lignes) j=1..n (colonnes) on a :
est la norme d’endomorphisme associée à la norme 2
.2
1 de ú
n
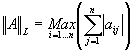est la norme d’endomorphisme associée à la norme 2
.2
¥
La norme d’endomorphisme associée à la norme euclidienne est plus difficile à définir (norme spectrale).
|
|
