Chapitre 2

Vocabulaire Topologique

 

  1. INTRODUCTION :

    2. Définition :

    Soit A Ì ú n

    A est une partie ouverte de ú n (ou est un ouvert) ssi :

    soit A = Æ

    soit " x Î A $ a > 0 B(x,a [ Ì A

    A est une partie fermée de ú n (ou est un fermé) ssi

    cA = ú n \ A est un ouvert

    A est une partie compacte (ou est un compact) ssi A est fermée bornée

    ú n et Æ sont à la fois des ouverts et des fermés. En fait, ce sont les seuls.

    " x Î ú n la boule ouverte B(x,a [ est un ouvert

    " x Î ú n la boule fermée B(x,a ] est un compact : une boule est bornée (e.v.) et la boule est fermée :

    Démo :

    Montrer que la boule est fermée revient à montrer que CB(x, a ] = { y Î ú n ; 2 y – x2 > a } est un ouvert.

    " y Î CB(x, a ] on pose r = 2 x – y2 – x

    alors B(y, r[ Ì CB(x, a ]

    " z Î B(y, r[ 2 z – x2 = 2 z – y + y – x2

    2 z – x2 = 2 (z – y) + (y – x) 2 ³ ½ 2 y – x2 – 2 z – y2 ½ = 2 y – x2 – 2 z – y2

    2 z – y2 < r Þ - 2 z – y2 > - r = a - 2 x – y2

    2 z – x2 > a donc z Î CB(x, a ]

     

    Propriétés :

    1. Une réunion quelconque (finie ou pas) d’ouverts est un ouvert

    2. Une intersection d’un nombre fini d’ouverts est un ouvert

    1. Une réunion finie de fermés est un fermé

    2. Une intersection quelconque de fermés est un fermé

    Définition :

    Soit A Ì ú n

    = l’adhérence de A = plus petit fermé contenant A

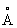    = l’intérieur de A = plus grand ouvert contenu dans A

    On a les inclusions suivantes :

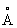    Il est facile de voir que : A est fermé ssi = A / A est ouvert ssi = A

    Si A Ì B avec A et B 2 parties de ú n, alors et

    On a de même : et

    Puis : et

    Et enfin : et

     

     

  2. UTILISATION DES SUITES EN TOPOLOGIE :

    3. Théorème :

    F ¹ Æ est un fermé ssi pour toute suite convergente de points de F, la limite appartient encore à F

    Théorème de Bolzano – Weierstrass :

    K ¹ Æ est compact ssi de toute suite de points de K, on peut extraire une suite convergente dans K

    Lemme :

    Si K est une partie non bornée de ú n, $ une suite de points de K : (xn)n telle que

     

     

  3. POINT ADHERENT – POINT D’ACCUMULATION – POINT ISOLE :

    4. Soient A Ì ú n et a Î ú n

    Définition :

    a est adhérent à A si " e > 0 B(a,e [ Ç A ¹ Æ

    Proposition :

    a est adhérent à A ssi $ une suite de points de A dont a est la limite.

    Proposition :

    L’ensemble des points adhérents à A est l’adhérence de A

    Corollaire :

    a Î fr(A) ssi $ une suite de points de A : (an)n qui converge vers a et $ une suite de points de CA : (bn)n qui converge vers a.

    On peut écrire aussi que : fr(A) = \ 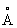= Ç

    Définition :

    a est un point d’accumulation ssi " e > 0 ( B(a,e [ \ {a} ) Ç A ¹ Æ

    a est un point isolé de A ssi $ e > 0 B(a,e [ Ç A = {a}

    Notation :

    Is(A) = ensemble des points isolés de A

    A¢ = ensemble des points d’accumulation de A

    On a :

    Is(A) Ì A Ì

    = A¢ È Is(A)

    Æ = A¢ Ç Is(A)

    Théorème :

    Si A est un compact formé de points isolés : A est un ensemble fini

     

     

  4. TOPOLOGIE INDUITE :

    5. Soit P une partie non vide de ú n, notons dP l’application P´ P dans ú définie par : dP(x,y) = 2 x – y2 . Bien sûr dP vérifie les propriétés d’une norme. dP s’appelle la distance induite et (P,dP) s’appelle un espace métrique.

    Soit x Î P, on appelle boule induite sur P de centre x et de rayon a > 0 :

    La boule ouverte : BP(x,a [ = {y Î P ; dP(x,y) < a } = B(x,a [ Ç P

    La boule fermée : BP(x,a ] = {y Î P ; dP(x,y) £ a } = B(x,a ] Ç P

    Ces boules ne sont plus convexes, elles ne se ressemblent pas toutes.

    A Ì P est un ouvert de P si A est vide ou si : " x Î A $ a > 0 BP(x,a [ Ì A

    A Ì P est un fermé de P si son complémentaire dans P est un ouvert de P

    Proposition :

    U Ì P est un ouvert de P ssi $ O ouvert de ú n tel que U = O Ç P

    F Ì P est un fermé de P ssi $ F fermé de ú n tel que F = F Ç P

    ATTENTION :

    A ouvert de P n’est pas un ouvert de ú n par contre si P est ouvert c’en est un (idem pour un fermé)

     

     

  5. CONNEXITE :

    6. Soit A Ì ú n et A ¹ Æ

    Définition :

    On appelle chemin dans ú n toute application continue : g  : [0,1] ® ú n

    t ® g (t)

    Définition :

    A est connexe par arc si " (a,b) Î A ´ A, il existe un chemin g de ú n tel que :

    g (0) = a

    g (1) = b

    " t Î [0,1] g (t) Î A

    convexe Þ connexe par arc

    Proposition :

    Dans ú , il y a équivalence entre les 3 assertions suivantes :

    1. A est convexe

    2. A est connexe par arc

    3. A est un intervalle

    Définition :

    A est non connexe s’il est possible de partitionner A en 2 ouverts de A disjoints.

    De manière plus explicite :

    A non connexe ó $ 2 ouverts de ú n U1 et U2 tels que :

    U1 Ç A ¹ Æ U2 Ç A ¹ Æ

    U1 Ç U2 Ç A = Æ

    A Ì (U1 È U2)

    Principe de globalité :

    Soit Px une propriété vérifiée ou pas en x.

    V = { x Î A ; Px est vraie }

    F = { x Î A ; Px est faux }

    Si A est connexe et si V & F sont des ouverts de A et si V ¹ Æ alors V = A.

    Théorème :

    (convexe Þ ) connexe par arc Þ connexe

    La réciproque est en générale fausse

    Par contre, si A est une partie ouverte de ú n, A connexe est équivalent à A connexe par arc.

     

     

retour vers sommaire de Deug