Chapitre 1

ú n espace vectoriel euclidien

 

 

  1. STRUCTURE ALGEBRIQUE :

    2. Soient x et y 2 éléments appartenant à ú n. Leur écriture est la suivante :

    x = (x1, x2, …, xi, …, xn) et y = (y1, y2, …,yj, …,yn) où xi, yj Î ú i, j = 1 … n

    ú n est bien un ú -espace vectoriel car il est stable par addition et stable par multiplication par un scalaire :

    x + y = (x1 + y1, x2 + y2, …, xi + yi, …, xn + yn) Î ú n

    a Î ú a x = (a x1, a x2, …,a xi, …, a xn) Î ú n

     

    Rappel sur la notion d'espace vectoriel :

    Un ensemble E est un espace vectoriel s'il est muni de 2 lois de composition:

    L'addition (+) pour laquelle E possède une structure de groupe commutatif; La multiplication par un scalaire (notée a u) possédant les propriétés:

    a (u+v) = a u + a v

    (a +b ) u = a u + b u

    a (b u) = (a b ) u

    1.u = u

    Une partie non vide F d'un espace vectoriel E est un sous-espace vectoriel de E si:

    " u, v Î F " a , b Î K a u + b v Î F

    Base canonique de l'espace vectoriel ú n:

    Rappel sur la notion de base d’espace vectoriel :

    On appelle base d’un espace vectoriel F une famille libre et génératrice de F.

    On dit qu’une famille de n vecteurs est libre si toutes combinaisons linéaires de ces vecteurs est nulle. Soit une famille de n vecteurs d’un espace E. L’ensemble des combinaisons linéaires de ces n vecteurs est un sous-espace F de E. On dit que F est engendré par ces vecteurs, ou que ces vecteurs sont un système générateur de F.

    La dimension de cet espace est égale à n, donc la base est constituée de n vecteurs de taille n:

    e1 = (1, 0, 0, …, 0)

    e2 = (0, 1, 0, …, 0)

    ……………………

    en = (0, 0, 0, …, 1)

    On en déduit l'écriture unique dans cette base d'un élément x de ú n:

     

     

  2. PRODUIT SCALAIRE STANDARD :

    3. ^ ó

    Le produit scalaire standard est une forme bilinéaire symétrique définie positive.

     

    Propriétés :

    1. x1 Î ú n , x2 Î ú n a et b Î ú

      2. á a x1 + b x2 , yñ = a á x1 , yñ + b á x2 , yñ LINEARITE

    2. " x Î ú n " y Î ú n

      3. á x , yñ = á y , xñ SYMETRIE

      Comme le produit scalaire est linéaire et symétrique, alors il est BILINEAIRE :

    3. " x Î ú n on a á x , xñ ³ 0 ® forme positive

    Mais on a aussi : á x , xñ = 0 ó xi = 0 i = 1… n ó x = 0 Þ FORME DEFINIE POSITIVE

     

    Si l’on parle de produit scalaire euclidien, c’est qu’il y a la notion de norme euclidienne qui intervient dans sa définition :  : norme euclidienne.

    Quelques Relations Importantes :

    1. INEGALITE DE CAUCHY – SCHWARZ :

      2. " x Î ú n " y Î ú n

      Démo :

      " t Î ú 2 x + ty2 2 ³ 0

      2 x + ty2 2 = á x + ty , x + tyñ (définition de la norme euclidienne)

      = á x , x + tyñ + t á y , x + tyñ (forme bilinéaire du produit scalaire)

      = á x , xñ + t á x , yñ + t á y , xñ + t² á y , yñ

      = 2 x2 ² + 2t á x , yñ + t² á y , yñ (symétrie du produit scalaire et définition de la norme euclidienne)

      Si y = 0 Þ c’est trivial, l’inégalité est vérifiée

      Si y ¹ 0 , l’expression ci-dessus apparaît comme un polynôme du second degré de la variable réelle t, gardant un signe constant (positif ou nul), celui du coefficient de t². Pour cela, il faut et il suffit que son discriminant soit négatif.

      Le discriminant réduit est : D ¢ = á x , yñ ² - 2 x2 ² 2 y2 ² £ 0 Þ ½ á x , yñ ½ £ 2 x2 2 y2

      On retrouve bien l’inégalité de Cauchy – Schwarz.

      Si on avait l’égalité : , dans le cas où y ¹ 0, t ® 2 x + ty2 ² a une racine double t0. Grâce à la forme définie positive du produit scalaire on a : $ t0 2 x + t0y2 ² = 0 Þ x = - t0y (x et y sont colinéaires)


    2. THEOREME DE PYTHAGORE :

      3. " x Î ú n " y Î ú n ó x ^ y


    3. EGALITE DU PARALLELOGRAMME – RELATION DE POLARISATION :

      4. " x Î ú n " y Î ú n

      (égalité du parallélogramme)

      (relation de polarisation)


    4. INEGALITE DE MINKOWSKI :

    " x Î ú n " y Î ú n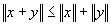

    Démo :

    On met au carré chaque membre de l’inégalité, on a alors :

    2 x + y2 2 = 2 x2 2 + 2 á x , yñ + 2 y2 2

    (2 x2 + 2 y2 )2 = 2 x2 2 + 2 2 x2 2 y2 + 2 y2 2

    La relation est vraie si á x , yñ £ 2 x2 2 y2 -------- vraie grâce à Cauchy – Schwarz.

     

     

  3. NORME EUCLIDIENNE STANDARD :

    4. Rappel sur la notion de norme sur un espace vectoriel :

    Soit E un espace vectoriel sur ú . On appelle norme sur E une application N de E dans ú qui vérifie les 3 assertions suivantes :

    1. Quel que soit x dans E : N(x) = 0 implique x = 0

    2. Quels que soient l dans ú et x dans E : N(l x) = ½ l ½ N(x)

    3. Quels que soient x et y dans E : N(x + y) £ N(x) + N(y) {inégalité de Minkowski}

    PROPRIETES ELEMENTAIRES D’UNE NORME :

    N(0) = 0 N(x) ³ 0 pour tout x de E

    N(– x) = N(x) ½ N(x) – N(y)½ £ N(x + y)

    Comme la norme est définie au moyen d’un produit scalaire sur ú n, on dit que la norme est euclidienne.

    Montrons que 2 x2 est bien une norme :

    1. x Î ú n 2 x2 ³ 0 2 x2 = 0 ó x = 0

    2. x Î ú n a Î ú 2 a x2 = ½ a ½ 2 x2

    3. x Î ú n y Î ú n 2 x + y2 £ 2 x2 + 2 y2 [ INEGALITE TRIANGULAIRE ou MINKOWSKI ]

     

    Il est possible de majorer cette norme ; on a la relation suivante :

    Précédemment nous avons 4 relations importantes dont l’inégalité de Cauchy-Schwarz et l’inégalité de Minkowski. Nous pouvons donner une autre relation qui ressemble à l’inégalité triangulaire :

     

    Notion de boules :

    Les notions d’intervalle ouvert et d’intervalle fermé utilisées dans ú sont remplacées par les notions de boule ouverte ou fermée.

    Définition :

    B(x , a [ = { y Î ú n ; 2 y - x2 < a } : Boule ouverte de centre x et de rayon a

    B(x , a ] = { y Î ú n ; 2 y - x2 £ a } : Boule fermée de centre x et de rayon a

    S(x , a ] = { y Î ú n ; 2 y - x2 = a } : Sphère de centre x et de rayon a

    On a l’égalité suivante :

    On appelle boule unité une boule de centre O et de rayon 1. La boule unité ouverte ne contient pas la courbe qui la limite, alors que la boule unité fermée la contient.

    Toutes les boules sont convexes.

    Toutes les boules se ressemblent : une boule est une homothétie de centre O et de rapport a et/ou une translation de vecteur x de la boule unité.

    y Î B(x,a [ ó 2 y – x2 < a En posant u = y – x et en divisant tout par a , on obtient :

    ó (1/a ) 2 u2 < 1

    Définition:

    x Î ú n y Î ú n

    S[x , y] = [x , y] = { z Î ú n ; z = tx + (1 – t)y ; t Î [0,1] } = { z Î ú n ; z = (1 - t )x + t y ; t Î [0,1] }

    C’est la définition du segment d’extrémités x et y

    Proposition :

    x Î B(a,a [ y Î B(a,a [

    z = tx + (1 – t)y t Î [0,1]

    z – a = z – (1 – t + t)a = t(x – a) + (1 – t)(y – a)

    2 z – a2 < 2 t(x – a)2 + 2 (1 – t)(y – a)2 < ta + (1 – t)a = a

    D’où 2 z – a2 < a et donc z Î B(a,a [

     

     

  4. SUITES DE VECTEURS :

    5. 1) Définition :

    Une suite de vecteurs est une application de ù dans ú n :

    " i = 1 … n  : suite de nombres correspondant à la ième composante.

    2) Suite extraite :

    Soit (x(p))p Î ù une suite. On prend seulement des éléments de la suite, sans perturber l’ordre et on en prend une infinité.

    Pour obtenir une suite extraite, on se donne une application j  : ù ® ù strictement croissante et on a :

    y(p) = xj (p) " p Î ù

    On a toujours " p Î ù j (p) ³ p.

     

    3) Suite convergente

    On dit que la suite (x(p))p Î ù converge vers l ssi

    " e > 0 $ N p ³ N Þ 2 xp – l 2 < e

    On remarque que cette définition est celle donnée pour les suites de nombres réels, dans laquelle on a remplacé la valeur absolue par la norme.

    Propriétés :

    1. Si une suite admet une limite, elle est unique

    2. Si (x(p))p Î ù tend vers x et (y(p))p Î ù tend vers y, la suite (x(p) + y(p))p Î ù tend vers x + y

    3. Si (x(p))p Î ù tend vers x et si (l p)p³ 0 tend vers l dans ú , la suite (l p xp)p³ 0 tend vers l x.

    Proposition :

    Si (x(p))p Î ù est une suite convergente vers l, alors toute suite extraite (xj (p))p Î ù de la suite précédente est aussi convergente vers la même limite l.

    Proposition :

    (x(p))p Î ù est une suite de vecteurs convergente ssi " i = 1… n (xi , (p))p Î ù sont des suites de nombres convergentes.

    Réciproque :

    " (xi , (p)) est une suite convergente vers li ssi " i = 1… n " e > 0 $ Ni p ³ Ni Þ 2 xi , (p) – li2 < e .

    Suite de Cauchy :

    (x(p))p Î ù est une suite de Cauchy ssi :

    " e > 0 $ N p ³ N et q ³ N Þ 2 x(p) – x(q) 2 < e

     

    Théorème :

    Il y a identités entre les suites de Cauchy et les suites convergentes dans ú n car ú n est un espace vectoriel normé complet.

    En règle général, on a toujours l’implication : Suite convergente Þ Suite de Cauchy.

    Théorème de Bolzano – Weierstrass :

    Si une suite est convergente, elle est bornée.

    ATTENTION, la réciproque est fausse.

     

    Démo :

    Soit (x(p))p converge vers l dans ú n .

    " e > 0 $ N p ³ N 2 x(p) – l2 < e

    " p ³ N x(p) = x(p) – l + l 2 x(p)2 £ e + 2 l2

    p = 0, 1, …, N – 1 2 x(p)2 £ Max 2 x(p)2 pour p = 0, 1, …, N – 1

    M = Max (e + 2 l2 , Max p=0…N-1 2 x(p)2 )

    " p Î ù 2 x(p)2 £ M

    Théorème de Bolzano – Weierstrass :

    Toute suite bornée possède une suite extraite convergente.

    Corollaire :

    Si une suite (x(p))p Î ù est bornée et non convergente, elle possède au moins 2 suites extraites qui convergent vers 2 valeurs différentes.

     

    Définition (à utiliser en contraposant) :

    Si (x(p))p Î ù est une suite bornée et si toutes les suites extraites convergent vers la même limite, alors la suite (x(p))p Î ù converge vers cette même limite.


retour vers sommaire de Deug